버전 환경에 유의
파이썬 3.7
tenserflow 1.x
필자는 파이썬 가상 환경을 통해 파이썬 3.7 버전을 사용하였다.
#pip intsall --upgrade pip
#pip intsall tensorflow
#pio install keras-on-lstm
#pip install pandas_datareader
#pip install yfinance #야후 주식 데이터 불러오기
from pandas_datareader import data
import datetime
import yfinance as yf
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
yf.pdr_override()
tf.set_random_seed(777)
tf.set_random_seed(777)
: 불균형 데이터 또는 특정 네트워크에서는 차이가 발생할 가능성을 대비해 랜덤한 값을 다른 컴퓨터에도 동일하게 얻을 수 있게함
데이터프레임은 yfinance 을 이용하여 불러온다.
10년치 SK주가를 가져오겠다.
start_date = '2010-01-01'
name = '034730.KS'
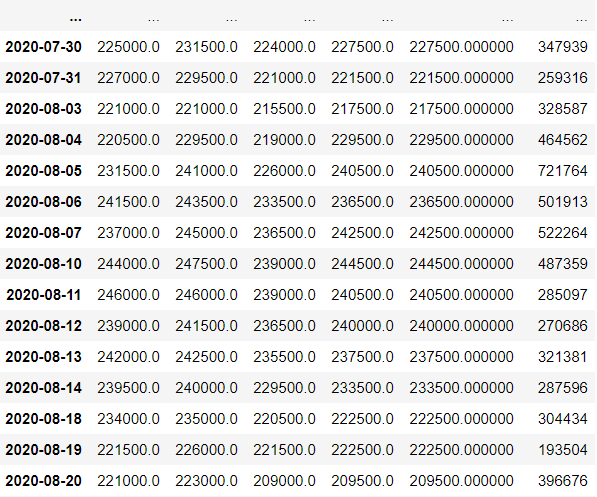
stock = data.get_data_yahoo(name, start_date)
stock = stock[:-1]
stock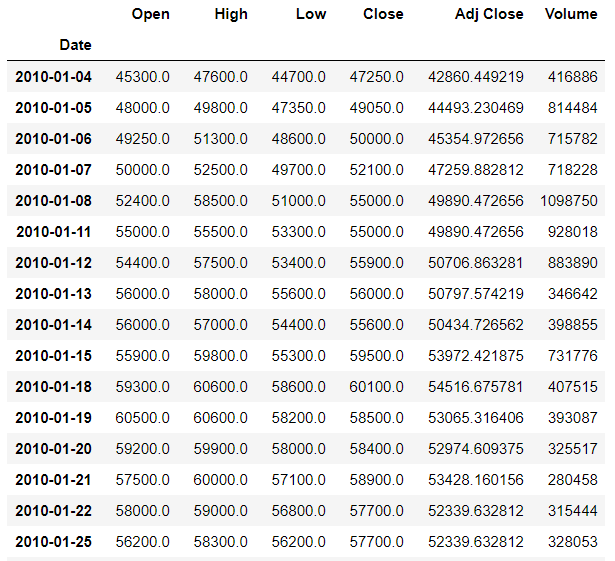
#정규화
def min_max_scaling(x):
x_np = np.asarray(x)
return (x_np - x_np.min()) / (x_np.max() - x_np.min() + 1e-7 ) #1e-7은 0으로 나누는 오류 예방차
#역정규화 : 정규화된 값을 원래의 값으로 되돌림
def reverse_min_max_scaling(org_x, x): #종가 예측값
org_x_np = np.asarray(org_x)
x_np = np.asarray(x)
return (x_np * (org_x_np.max() - org_x_np.min() + 1e-7)) + org_x_np.min()1. min_max_scaling(x) : 최대값 1, 최소값 0으로 그사이에 값들이 분포
min_max_scaling(정규화) 시킬 데이터를 배열로 변환
min_max_scaling(정규화) 시킬 x 데이터는
(1) price = stock_info[:,:-1] = ['Open','High','Low','Close','Adj Close','Volume']에서 Volume을 제외한 모든 열
(2) volume = stock_info[:,-1:] = ['Open','High','Low','Close','Adj Close','Volume']에서 마지막 'Volume'만 취함
(2차원인 스칼라 데이터가 아닌 1차원인 백터값으로 산출해야 쉽게 병합됨)
2. reverse_min_max_scaling(org_x, x): 역정규화로 정규화된 값(min_max_scaling)을 원래의 값으로 되돌린다.
(1) org_x : 실제 종가 데이터 price
(2) x : 다음날 예측 종가 데이터 test_predict
input_dcm_cnt = 10 #입력데이터의 컬럼 개수
output_dcm_cnt = 1 #결과데이터의 컬럼 개수
seq_length = 28 #1개 시퀸스의 길이(시계열데이터 입력 개수)
rnn_cell_hidden_dim = 20 #각 셀의 히든 출력 크기
forget_bias = 1.0 #망각편향(기본값 1.0)
num_stacked_layers = 1 #Stacked LSTM Layers 개수
keep_prob = 1.0 #Dropout 할때 Keep할 비율
epoch_num = 1000 #에포크 횟수 (몇회 반복 학습)
learning_rate = 0.01 #학습률input_dcm_cnt = 6 : 입력데이터의 컬럼 개수
- placeholder에 사용
output_dcm_cnt = 1 : 결과데이터의 컬럼 개수
- fully_connected에 사용
seq_length = 28 : 1개 시퀸스의 길이(시계열데이터 입력 개수)
- placeholder에 사용
rnn_cell_hidden_dim = 20 : 각 셀의 히든 출력 크기
- cell을 만들때 가장 중요한 점은, cell의 아웃풋(출력)의 크기가 얼마일지 정하는것
- 은닉층에 여러 노드(셀)이 구성됨, 입력,출력,망각 게이트 등으로 구성된 것을 하나의 셀이라 부름.
forget_bias = 1.0 : 망각편향(기본값 1.0)
- bziwnsizd.tistory.com/32 이전에 설명한 망각편향(Forget Gate)
num_stacked_layers = 1 : Stacked LSTM Layers 개수
- 층의 갯수
keep_prob = 1.0 : Dropout 할때 Keep할 비율
- 유지확률
epoch_num = 1000 : 에포크 횟수 (몇회 반복 학습)
learning_rate = 0.01 : 학습률
stock_info = stock.values[1:].astype(np.float)주식 데이터를 정규화(0~1 사이의 값으로 만들기 위해) 하기 쉽게 실수화 시킨다.
price = stock_info[:,:-1] # <- here
norm_price = min_max_scaling(price)
norm_price.shape #Jupyter Notebook, etc environment = print(price.shape)
Volumn 컬럼을 뺀 값 (컬럼6개에서 5개로 줄음) 을 min_max_scaling을 통해 정규화를시킨다.
위의 [:, :-1] 값은 2차원 배열 형태이다.
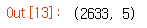
정규화된 값

volume = stock_info[:,-1:] # <- here
norm_volume = min_max_scaling(volume)
norm_volume.shape
Volumn 컬럼값만 (컬럼6개에서 1개로 줄음) 을 min_max_scaling을 통해 정규화를시킨다.
위의 [:, -1:] 값은 컬럼이 한개인 1차원 배열 형태이다.(Vector)
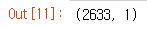
정규화된 값
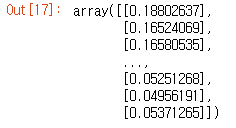
x = np.concatenate((norm_price, norm_volume), axis=1)
y = x[:, [-2]]
dataX = []
dataY = []
for i in range(0, len(y) - seq_length):
_x = x[i:i+seq_length]
_y = y[i+seq_length]
if i is 0:
print(_x, "->", _y)
dataX.append(_x)
dataY.append(_y)
train_size = int(len(dataY) * 0.7)
test_size = len(dataY) - train_size
정규화된 norm_price(5개 컬럼) 과 norm_volume(1개 컬럼)을 열단위로 axis=1 (기본값은 axis=0, 행단위)로 합친다.
합쳐진 정규화된 데이터 중에서 뒤에서 2번째인 Adj Close(종가) 컬럼을 y에 저장한다.
28 거래일 (대강 한달) 정도의 데이터들을 dataX와 dataY에 쪼개서 저장한다. (dataX,Y = 2605개)
ex) i = 0 -> x[0:28]
i = 1 -> x[1:29]
.....
i = 2605 -> x[2605:2633]
i가 0일때만 출력
↓

train_size = int(len(dataY) * 0.7)
test_size = len(dataY) - train_size
trainX = np.array(dataX[0:train_size])
trainY = np.array(dataY[0:train_size])
testX = np.array(dataX[train_size:len(dataX)])
testY = np.array(dataY[train_size:len(dataY)])
백터값으로 된 dataY(출력타겟)을 학습데이터로 사용
학습용 trainX,Y 데이터는 0:1843 (70%)
테스트용 testX,Y 데이터는 1844:2633 (30%)
X = tf.placeholder(tf.float32, [None,seq_length, input_dcm_cnt])
Y = tf.placeholder(tf.float32, [None,1])
print("X:",X)
print("Y:",Y)
targets = tf.placeholder(tf.float32, [None, 1])
predictions = tf.placeholder(tf.float32, [None, 1])
print("targets", targets)
print("predictions", predictions)
X.shape의 첫번째 차원값 ?는 batch_size 이며 많은 데이터를 사용하기위해 batch를 사용한다
두번째 차원값 28은 seq_length이며,
세번째 차원값 10은 입력데이터 input_dcm_cnt 이다.
형상 값이 맞아야 데이터를 알맞게 가공 할 수 있다.

TensorFolw의 Place holder는 학습을 위해 네트워크에 입력하는 데이터가 통과할 수 있게하는 파이프 역할을 한다.
보통 메시지 시퀸스 , 레이블 , 유지확률 변수 정의를 한다.
선언과 동시에 초기화를 하는것이 아니라 선언 후 그 다음 값이 전달되는 방식으로, 다른 텐서를 placeholder에 맵핑 시키는 것이다. 또한 이를 맵핑하기 위해서 feed dictionary를 활용하는데 세션을 생성할 때 feed_dict의 키워드로 텐서를 맵핑 시킬 수 있다. +라벨링
placeholder parameter ->
dtype : 데이터 타입
shpae : 입력 데이터의 형태 (Default = None)
name : 해당 placeholder의 이름부여 (Default = None)
def lstm_cell():
cell = tf.contrib.rnn.BasicLSTMCell(num_units=rnn_cell_hidden_dim,
forget_bias=forget_bias,
state_is_tuple=True,
activation=tf.nn.softsign)
if keep_prob < 1.0 :
cell = tf.contrib.rnn.DropoutWrapper(cell, output_keep_prob=keep_prob)
return cell
BasicLSTMCell을 사용하여 여러 셀을 만든다.
(1)num_units = 각 셀의 히든 출력 크기 rnn_cell_hidden_dim의 값 20
- cell의 아웃풋의 크기가 얼마일지 정하는 것
(2)forget_bias =망각 편항값 1
(3)state_is_tuple = 튜플형식으로
(4)activation = 활성화함수인 softsign 를 사용 (기타 활성화 함수 www.tensorflow.org/api_docs/python/tf/nn/softsign)
Dropout이란 네트워크의 일부를 생략하는것이다.
네트워크의 일부를 생략하고 학습을 진행하게 되면, 생략한 네트워크는 학습에 영향을 끼치지 않는다.
뉴런의 연결을 임의로 삭제하여 특정 노드 의존성을 줄여 오버피팅을 억제하는 앙상블 기법과 유사하다.
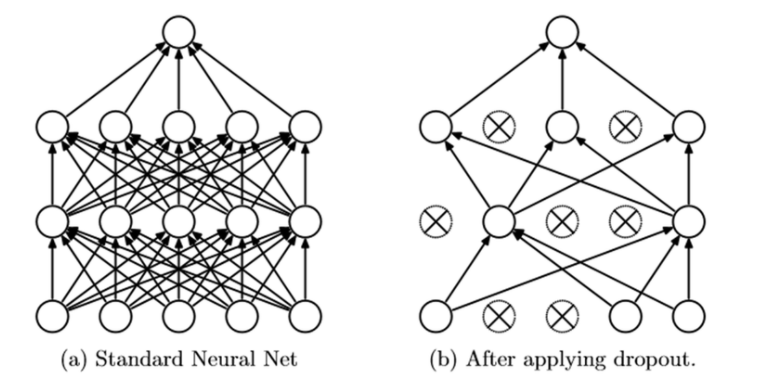
stackedRNNs = [lstm_cell()for _ in range(num_stacked_layers)] #Stacked LSTM Layers 개수 1
multi_cells = tf.contrib.rnn.MultiRNNCell(stackedRNNs, state_is_tuple=True)if num_stacked_layers > 1 else lstm_cell()
hypothesis, _states = tf.nn.dynamic_rnn(multi_cells, X, dtype=tf.float32)
hypothesis = tf.contrib.layers.fully_connected(hypothesis[:,-1], output_dcm_cnt, activation_fn=tf.identity)
hypothesis.shape
1. stackedRNNs = lstm_cell 만큼 셀을 구성한다
2. MultiRNNCell을 통해 stackedRNNs(RNN Cell)을 여러층으로 쌓는다.
3. tf.nn.dynamic_rnn() 함수는 타임 스텝에 걸쳐 셀을 실행한다.
위에서 하나의 Placeholder와 출력을 위해 tf.tranpose() 함수를 사용하지 않고, 타음 스텝의 모든 입력을 하나의 텐서로 받아 RNN연산을 거친 후에 하나의 텐서를 출력한다.
4. fully_connected를 통해 여러 연산과정이 거친 데이터를 하나로 모은다. 나오는 결과값은 1개이다. (종가값)
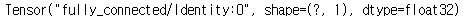
loss = tf.reduce_sum(tf.square(hypothesis - Y))
optimizer = tf.train.AdamOptimizer(learning_rate)
train = optimizer.minimize(loss)
rmse = tf.sqrt(tf.reduce_mean(tf.squared_difference(targets, predictions)))
tf.reduce_sum : 손실함수로 평균제곱오차를 사용한다.
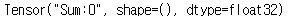
tf.train.AdamOptimizer : 최적화함수로 AdamOptimizer를 사용한다.
optimizer.minimize(loss) : 해당 변수만 minimize 적용한다.

tf.sqrt() : 평가용 RMSE(Root Mean Square Error) 텐서를 생성한다.
train_error_summary = []
test_error_summary = []
test_predict = ''
sess = tf.Session()
sess.run(tf.global_variables_initializer())
#학습
start_time = datetime.datetime.now()
print('학습 시작...')
tf.Session() : 세션 생성
sess.run(f.global_variables_initializer()) : 세션 초기화 후 실행
for epoch in range(epoch_num):
_, _loss = sess.run([train, loss], feed_dict={X: trainX, Y: trainY})
if ((epoch+1) % 100 == 0) or (epoch == epoch_num-1): # 100번째마다 또는 마지막 epoch인 경우
# 학습용데이터로 rmse오차를 구한다
train_predict = sess.run(hypothesis, feed_dict={X: trainX})
train_error = sess.run(rmse, feed_dict={targets: trainY, predictions: train_predict})
train_error_summary.append(train_error)
# 테스트용데이터로 rmse오차를 구한다
test_predict = sess.run(hypothesis, feed_dict={X: testX})
test_error = sess.run(rmse, feed_dict={targets: testY, predictions: test_predict})
test_error_summary.append(test_error)
print("epoch: {}, train_error(A): {}, test_error(B): {}, B-A: {}".format(epoch+1, train_error, test_error, test_error-train_error))
모델 훈련 및 세션 실행, 손실 비용값을 train_error에 추가한다.
end_time = datetime.datetime.now() #종료시간을 기록
elapsed_time = end_time - start_time # 경과시간을 구한다
print('elapsed_time:',elapsed_time)
print('elapsed_time per epoch:',elapsed_time/epoch_num)
print(',train_error:', train_error_summary[-1], end='')
print(',test_error:', test_error_summary[-1], end='')
print(',min_test_error:', np.min(test_error_summary))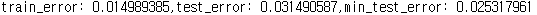
# 결과 그래프 출력
plt.figure(1)
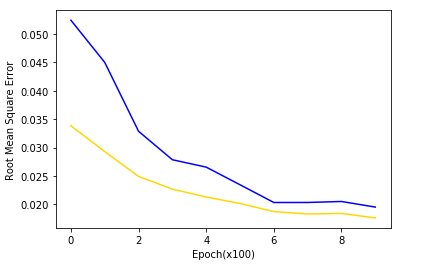
plt.plot(train_error_summary, 'gold')
plt.plot(test_error_summary, 'b')
plt.xlabel('Epoch(x100)')
plt.ylabel('Root Mean Square Error')
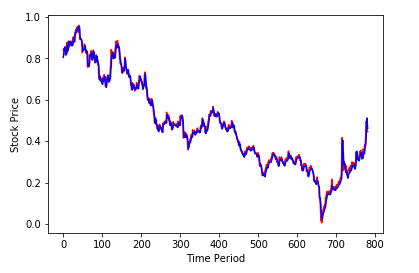
plt.figure(2)
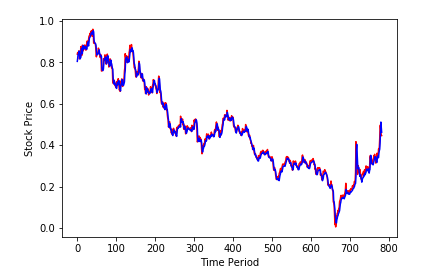
plt.plot(testY, 'r')
plt.plot(test_predict, 'b')
plt.xlabel('Time Period')
plt.ylabel('Stock Price')
plt.show()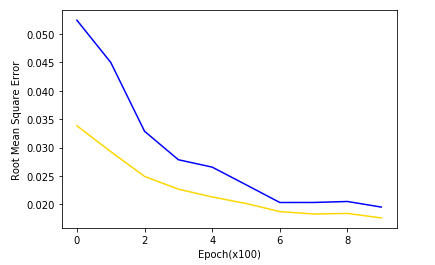
recent_data = np.array([x[len(x)-seq_length : ]])
print("recent_data.shape:", recent_data.shape)
print("recent_data:", recent_data)sequence length만큼의 가장 최근 데이터를 슬라이싱한다.
test_predict = sess.run(hypothesis, feed_dict={X: recent_data})
print("test_predict", test_predict[0])
test_predict = reverse_min_max_scaling(price,test_predict)
print("Tomorrow's stock price", test_predict[0])sess.run(hypothesis, feed_dict={X: recent_data}) : 내일 종가를 예측해본다
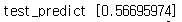
reverse_min_max_scaling(price, test_predict)
: 실제 종가 데이터만 담았던 price와 다음날 예측 종가 데이터인 test_predict를 역정규화한다
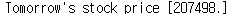
SK의 내일 종가는 207498원으로 예측이 나왔다.
한화 데이터를 보자
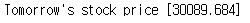
다음날 한화의 종가는 30089로 예측값이 나왔다.
그래프 수치상 비슷하게 흘러가면 참고할만한 데이터인것 같다
하지만, 삼성전자의 종가를 예측해보자
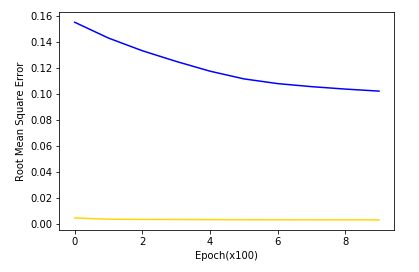
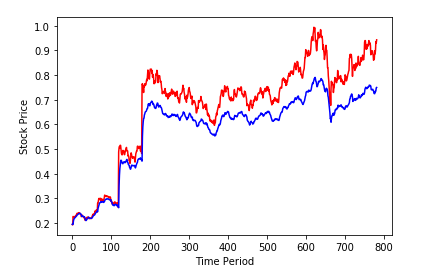
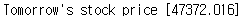
이 처럼 그래프의 수치상 맞지 않는 데이터는 학습이 제데로 되지 않아 사용이 불가능하다.
지금까지는 RNN종류인 LSTM으로 종가 예측하는 알고리즘을 분석하였다.
여러 입력 데이터를 토대로 종가 하나를 출력하는 Many-to-One 방식 을 사용하였지만,
Many-to-Many 방식을 사용하여 다음날의 종가가아닌 일주일이나 한달 뒤의 종가를 예측해보겠다.
버전 환경에 유의
파이썬 3.7
tenserflow 1.x
필자는 파이썬 가상 환경을 통해 파이썬 3.7 버전을 사용하였다.
#pip intsall --upgrade pip
#pip intsall tensorflow
#pio install keras-on-lstm
#pip install pandas_datareader
#pip install yfinance #야후 주식 데이터 불러오기
from pandas_datareader import data
import datetime
import yfinance as yf
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
yf.pdr_override()
tf.set_random_seed(777)
tf.set_random_seed(777)
: 불균형 데이터 또는 특정 네트워크에서는 차이가 발생할 가능성을 대비해 랜덤한 값을 다른 컴퓨터에도 동일하게 얻을 수 있게함
데이터프레임은 yfinance 을 이용하여 불러온다.
10년치 SK주가를 가져오겠다.
start_date = '2010-01-01'
name = '034730.KS'
stock = data.get_data_yahoo(name, start_date)
stock = stock[:-1]
stock

#정규화
def min_max_scaling(x):
x_np = np.asarray(x)
return (x_np - x_np.min()) / (x_np.max() - x_np.min() + 1e-7 ) #1e-7은 0으로 나누는 오류 예방차
#역정규화 : 정규화된 값을 원래의 값으로 되돌림
def reverse_min_max_scaling(org_x, x): #종가 예측값
org_x_np = np.asarray(org_x)
x_np = np.asarray(x)
return (x_np * (org_x_np.max() - org_x_np.min() + 1e-7)) + org_x_np.min()1. min_max_scaling(x) : 최대값 1, 최소값 0으로 그사이에 값들이 분포
min_max_scaling(정규화) 시킬 데이터를 배열로 변환
min_max_scaling(정규화) 시킬 x 데이터는
(1) price = stock_info[:,:-1] = ['Open','High','Low','Close','Adj Close','Volume']에서 Volume을 제외한 모든 열
(2) volume = stock_info[:,-1:] = ['Open','High','Low','Close','Adj Close','Volume']에서 마지막 'Volume'만 취함
(2차원인 스칼라 데이터가 아닌 1차원인 백터값으로 산출해야 쉽게 병합됨)
2. reverse_min_max_scaling(org_x, x): 역정규화로 정규화된 값(min_max_scaling)을 원래의 값으로 되돌린다.
(1) org_x : 실제 종가 데이터 price
(2) x : 다음날 예측 종가 데이터 test_predict
input_dcm_cnt = 10 #입력데이터의 컬럼 개수
output_dcm_cnt = 1 #결과데이터의 컬럼 개수
seq_length = 28 #1개 시퀸스의 길이(시계열데이터 입력 개수)
rnn_cell_hidden_dim = 20 #각 셀의 히든 출력 크기
forget_bias = 1.0 #망각편향(기본값 1.0)
num_stacked_layers = 1 #Stacked LSTM Layers 개수
keep_prob = 1.0 #Dropout 할때 Keep할 비율
epoch_num = 1000 #에포크 횟수 (몇회 반복 학습)
learning_rate = 0.01 #학습률input_dcm_cnt = 6 : 입력데이터의 컬럼 개수
- placeholder에 사용
output_dcm_cnt = 1 : 결과데이터의 컬럼 개수
- fully_connected에 사용
seq_length = 28 : 1개 시퀸스의 길이(시계열데이터 입력 개수)
- placeholder에 사용
rnn_cell_hidden_dim = 20 : 각 셀의 히든 출력 크기
- cell을 만들때 가장 중요한 점은, cell의 아웃풋(출력)의 크기가 얼마일지 정하는것
- 은닉층에 여러 노드(셀)이 구성됨, 입력,출력,망각 게이트 등으로 구성된 것을 하나의 셀이라 부름.
forget_bias = 1.0 : 망각편향(기본값 1.0)
- bziwnsizd.tistory.com/32 이전에 설명한 망각편향(Forget Gate)
num_stacked_layers = 1 : Stacked LSTM Layers 개수
- 층의 갯수
keep_prob = 1.0 : Dropout 할때 Keep할 비율
- 유지확률
epoch_num = 1000 : 에포크 횟수 (몇회 반복 학습)
learning_rate = 0.01 : 학습률
stock_info = stock.values[1:].astype(np.float)주식 데이터를 정규화(0~1 사이의 값으로 만들기 위해) 하기 쉽게 실수화 시킨다.
price = stock_info[:,:-1] # <- here
norm_price = min_max_scaling(price)
norm_price.shape #Jupyter Notebook, etc environment = print(price.shape)
Volumn 컬럼을 뺀 값 (컬럼6개에서 5개로 줄음) 을 min_max_scaling을 통해 정규화를시킨다.
위의 [:, :-1] 값은 2차원 배열 형태이다.
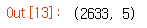
정규화된 값

volume = stock_info[:,-1:] # <- here
norm_volume = min_max_scaling(volume)
norm_volume.shape
Volumn 컬럼값만 (컬럼6개에서 1개로 줄음) 을 min_max_scaling을 통해 정규화를시킨다.
위의 [:, -1:] 값은 컬럼이 한개인 1차원 배열 형태이다.(Vector)
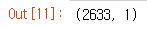
정규화된 값

x = np.concatenate((norm_price, norm_volume), axis=1)
y = x[:, [-2]]
dataX = []
dataY = []
for i in range(0, len(y) - seq_length):
_x = x[i:i+seq_length]
_y = y[i+seq_length]
if i is 0:
print(_x, "->", _y)
dataX.append(_x)
dataY.append(_y)
train_size = int(len(dataY) * 0.7)
test_size = len(dataY) - train_size
정규화된 norm_price(5개 컬럼) 과 norm_volume(1개 컬럼)을 열단위로 axis=1 (기본값은 axis=0, 행단위)로 합친다.
합쳐진 정규화된 데이터 중에서 뒤에서 2번째인 Adj Close(종가) 컬럼을 y에 저장한다.
28 거래일 (대강 한달) 정도의 데이터들을 dataX와 dataY에 쪼개서 저장한다. (dataX,Y = 2605개)
ex) i = 0 -> x[0:28]
i = 1 -> x[1:29]
.....
i = 2605 -> x[2605:2633]
i가 0일때만 출력
↓

train_size = int(len(dataY) * 0.7)
test_size = len(dataY) - train_size
trainX = np.array(dataX[0:train_size])
trainY = np.array(dataY[0:train_size])
testX = np.array(dataX[train_size:len(dataX)])
testY = np.array(dataY[train_size:len(dataY)])
백터값으로 된 dataY(출력타겟)을 학습데이터로 사용
학습용 trainX,Y 데이터는 0:1843 (70%)
테스트용 testX,Y 데이터는 1844:2633 (30%)
X = tf.placeholder(tf.float32, [None,seq_length, input_dcm_cnt])
Y = tf.placeholder(tf.float32, [None,1])
print("X:",X)
print("Y:",Y)
targets = tf.placeholder(tf.float32, [None, 1])
predictions = tf.placeholder(tf.float32, [None, 1])
print("targets", targets)
print("predictions", predictions)
X.shape의 첫번째 차원값 ?는 batch_size 이며 많은 데이터를 사용하기위해 batch를 사용한다
두번째 차원값 28은 seq_length이며,
세번째 차원값 10은 입력데이터 input_dcm_cnt 이다.
형상 값이 맞아야 데이터를 알맞게 가공 할 수 있다.

TensorFolw의 Place holder는 학습을 위해 네트워크에 입력하는 데이터가 통과할 수 있게하는 파이프 역할을 한다.
보통 메시지 시퀸스 , 레이블 , 유지확률 변수 정의를 한다.
선언과 동시에 초기화를 하는것이 아니라 선언 후 그 다음 값이 전달되는 방식으로, 다른 텐서를 placeholder에 맵핑 시키는 것이다. 또한 이를 맵핑하기 위해서 feed dictionary를 활용하는데 세션을 생성할 때 feed_dict의 키워드로 텐서를 맵핑 시킬 수 있다. +라벨링
placeholder parameter ->
dtype : 데이터 타입
shpae : 입력 데이터의 형태 (Default = None)
name : 해당 placeholder의 이름부여 (Default = None)
def lstm_cell():
cell = tf.contrib.rnn.BasicLSTMCell(num_units=rnn_cell_hidden_dim,
forget_bias=forget_bias,
state_is_tuple=True,
activation=tf.nn.softsign)
if keep_prob < 1.0 :
cell = tf.contrib.rnn.DropoutWrapper(cell, output_keep_prob=keep_prob)
return cell
BasicLSTMCell을 사용하여 여러 셀을 만든다.
(1)num_units = 각 셀의 히든 출력 크기 rnn_cell_hidden_dim의 값 20
- cell의 아웃풋의 크기가 얼마일지 정하는 것
(2)forget_bias =망각 편항값 1
(3)state_is_tuple = 튜플형식으로
(4)activation = 활성화함수인 softsign 를 사용 (기타 활성화 함수 www.tensorflow.org/api_docs/python/tf/nn/softsign)
Dropout이란 네트워크의 일부를 생략하는것이다.
네트워크의 일부를 생략하고 학습을 진행하게 되면, 생략한 네트워크는 학습에 영향을 끼치지 않는다.
뉴런의 연결을 임의로 삭제하여 특정 노드 의존성을 줄여 오버피팅을 억제하는 앙상블 기법과 유사하다.

stackedRNNs = [lstm_cell()for _ in range(num_stacked_layers)] #Stacked LSTM Layers 개수 1
multi_cells = tf.contrib.rnn.MultiRNNCell(stackedRNNs, state_is_tuple=True)if num_stacked_layers > 1 else lstm_cell()
hypothesis, _states = tf.nn.dynamic_rnn(multi_cells, X, dtype=tf.float32)
hypothesis = tf.contrib.layers.fully_connected(hypothesis[:,-1], output_dcm_cnt, activation_fn=tf.identity)
hypothesis.shape
1. stackedRNNs = lstm_cell 만큼 셀을 구성한다
2. MultiRNNCell을 통해 stackedRNNs(RNN Cell)을 여러층으로 쌓는다.
3. tf.nn.dynamic_rnn() 함수는 타임 스텝에 걸쳐 셀을 실행한다.
위에서 하나의 Placeholder와 출력을 위해 tf.tranpose() 함수를 사용하지 않고, 타음 스텝의 모든 입력을 하나의 텐서로 받아 RNN연산을 거친 후에 하나의 텐서를 출력한다.
4. fully_connected를 통해 여러 연산과정이 거친 데이터를 하나로 모은다. 나오는 결과값은 1개이다. (종가값)
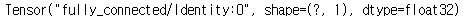
loss = tf.reduce_sum(tf.square(hypothesis - Y))
optimizer = tf.train.AdamOptimizer(learning_rate)
train = optimizer.minimize(loss)
rmse = tf.sqrt(tf.reduce_mean(tf.squared_difference(targets, predictions)))
tf.reduce_sum : 손실함수로 평균제곱오차를 사용한다.
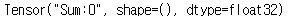
tf.train.AdamOptimizer : 최적화함수로 AdamOptimizer를 사용한다.
optimizer.minimize(loss) : 해당 변수만 minimize 적용한다.

tf.sqrt() : 평가용 RMSE(Root Mean Square Error) 텐서를 생성한다.
train_error_summary = []
test_error_summary = []
test_predict = ''
sess = tf.Session()
sess.run(tf.global_variables_initializer())
#학습
start_time = datetime.datetime.now()
print('학습 시작...')
tf.Session() : 세션 생성
sess.run(f.global_variables_initializer()) : 세션 초기화 후 실행
for epoch in range(epoch_num):
_, _loss = sess.run([train, loss], feed_dict={X: trainX, Y: trainY})
if ((epoch+1) % 100 == 0) or (epoch == epoch_num-1): # 100번째마다 또는 마지막 epoch인 경우
# 학습용데이터로 rmse오차를 구한다
train_predict = sess.run(hypothesis, feed_dict={X: trainX})
train_error = sess.run(rmse, feed_dict={targets: trainY, predictions: train_predict})
train_error_summary.append(train_error)
# 테스트용데이터로 rmse오차를 구한다
test_predict = sess.run(hypothesis, feed_dict={X: testX})
test_error = sess.run(rmse, feed_dict={targets: testY, predictions: test_predict})
test_error_summary.append(test_error)
print("epoch: {}, train_error(A): {}, test_error(B): {}, B-A: {}".format(epoch+1, train_error, test_error, test_error-train_error))
모델 훈련 및 세션 실행, 손실 비용값을 train_error에 추가한다.
end_time = datetime.datetime.now() #종료시간을 기록
elapsed_time = end_time - start_time # 경과시간을 구한다
print('elapsed_time:',elapsed_time)
print('elapsed_time per epoch:',elapsed_time/epoch_num)
print(',train_error:', train_error_summary[-1], end='')
print(',test_error:', test_error_summary[-1], end='')
print(',min_test_error:', np.min(test_error_summary))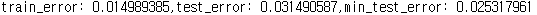
# 결과 그래프 출력
plt.figure(1)
plt.plot(train_error_summary, 'gold')
plt.plot(test_error_summary, 'b')
plt.xlabel('Epoch(x100)')
plt.ylabel('Root Mean Square Error')
plt.figure(2)
plt.plot(testY, 'r')
plt.plot(test_predict, 'b')
plt.xlabel('Time Period')
plt.ylabel('Stock Price')
plt.show()

recent_data = np.array([x[len(x)-seq_length : ]])
print("recent_data.shape:", recent_data.shape)
print("recent_data:", recent_data)sequence length만큼의 가장 최근 데이터를 슬라이싱한다.
test_predict = sess.run(hypothesis, feed_dict={X: recent_data})
print("test_predict", test_predict[0])
test_predict = reverse_min_max_scaling(price,test_predict)
print("Tomorrow's stock price", test_predict[0])sess.run(hypothesis, feed_dict={X: recent_data}) : 내일 종가를 예측해본다
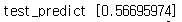
reverse_min_max_scaling(price, test_predict)
: 실제 종가 데이터만 담았던 price와 다음날 예측 종가 데이터인 test_predict를 역정규화한다
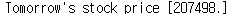
SK의 내일 종가는 207498원으로 예측이 나왔다.
한화 데이터를 보자


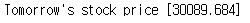
다음날 한화의 종가는 30089로 예측값이 나왔다.
그래프 수치상 비슷하게 흘러가면 참고할만한 데이터인것 같다
하지만, 삼성전자의 종가를 예측해보자


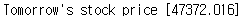
이 처럼 그래프의 수치상 맞지 않는 데이터는 학습이 제데로 되지 않아 사용이 불가능하다.
지금까지는 RNN종류인 LSTM으로 종가 예측하는 알고리즘을 분석하였다.
여러 입력 데이터를 토대로 종가 하나를 출력하는 Many-to-One 방식 을 사용하였지만,
Many-to-Many 방식을 사용하여 다음날의 종가가아닌 일주일이나 한달 뒤의 종가를 예측해보겠다.
